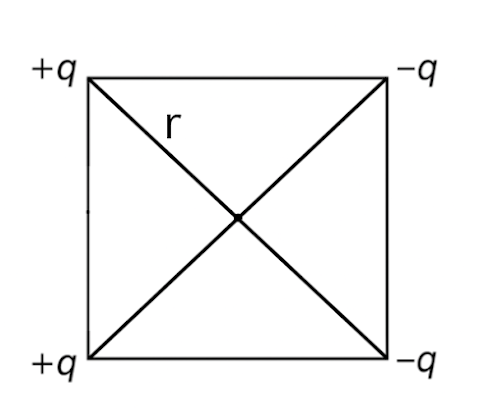
Four electric charges +q, +q, −q and −q are placed at the corners of a square of side 2 L (see figure). The electric potential at point A, midway between the two charges +q and +q, is ?

Four electric charges +q, +q, −q and −q are placed at the corners of a square of side 2 L (see figure). The electric potential at point A, midway between the two charges +q and +q, is ?

(a) \( \frac{1}{4\pi \varepsilon_0} \cdot \frac{2q}{L}(1 + \sqrt{5}) \)

(b) \( \frac{1}{4\pi \varepsilon_0} \cdot \frac{2q}{L} \left(1 + \sqrt{\frac{1}{5}} \right) \)

(c) \( \frac{1}{4\pi \varepsilon_0} \cdot \frac{2q}{L} \left(1 - \sqrt{\frac{1}{5}} \right) \)

(d) zero

Answer :  (c) \( \frac{1}{4\pi \varepsilon_0} \cdot \frac{2q}{L} \left(1 - \sqrt{\frac{1}{5}} \right) \)

\( V = \frac{kq}{r} \)

\( V = \frac{k(-q)}{r} \)

\( V_1 = \frac{1}{4\pi\varepsilon_0} \cdot \frac{q}{L} \)

\( V_2 = \frac{1}{4\pi\varepsilon_0} \cdot \frac{q}{L} \)

\( V_3 = \frac{1}{4\pi\varepsilon_0} \cdot \frac{-q}{\sqrt{5}L} \)

\( V_4 = \frac{-q}{4\pi\varepsilon_0 \sqrt{5}L} \)

\( V_{\text{total}} = V_1 + V_2 + V_3 + V_4 \)

\( = \frac{1}{4\pi\varepsilon_0} \cdot \frac{2q}{L} \left(1 - \frac{1}{\sqrt{5}} \right) \)