trial chatgpt codes
\[ \frac{F_{\text{electric}}}{F_{\text{gravity}}}\]
\[ \frac{\Delta L}{L} = ? \] \[ \text{Given: } \text{Hypotenuse } = L +
\Delta L, \quad \text{Opposite side } = x \] Using Pythagoras’ Theorem: \[
L^2 + x^2 = (L + \Delta L)^2 \] \[ L^2 + x^2 = \left( L \left(1 +
\frac{\Delta L}{L} \right) \right)^2 \] \[ L^2 + x^2 = L^2 \left(1 +
\frac{\Delta L}{L} \right)^2 \] Divide both sides by \( L^2 \): \[ 1 +
\frac{x^2}{L^2} = \left(1 + \frac{\Delta L}{L} \right)^2 \] \[ \sqrt{1 +
\frac{x^2}{L^2}} = 1 + \frac{\Delta L}{L} \] Using the approximation \(
\sqrt{1 + x} \approx 1 + \frac{x}{2} \) for small \( x \), we get: \[ 1 +
\frac{x^2}{2L^2} \approx 1 + \frac{\Delta L}{L} \] \[ \Rightarrow
\frac{\Delta L}{L} \approx \frac{x^2}{2L^2} \] \[ \boxed{\frac{\Delta
L}{L} = \frac{x^2}{2L^2}} \]
\[ \sum F = ma \]\[ 100 - \mu mg = ma \] \[ 100 - (0.5)(10)(10) = (10)a
\] \[ 50 = 10\hspace{2mm}a \] \[ a = 5 \, \text{m/s}^2 \]
In carbon monoxide molecule, the carbon and the oxygen atoms are separated by a distance 1.12 × $10^{−10}$m. The distance of the centre of mass, from the carbon atom is
In carbon monoxide molecule, the carbon and the oxygen atoms are separated by a distance 1.12 × 10−10 m. The distance of the centre of mass, from the carbon atom is
(a) $0.64 × 10^{−10} m$
(b) $0.56 × 10^{−10} m$
(c) $0.51 × 10^{−10} m$
(d) $0.48 × 10^{−10} m$
[NEET 1997]
\[M\; r_{cm}=m_1 \; r_1 + m_2 \; r_2\]
\[\left (12u+16u \right) \; x = 12u \; (0) + 16u \left (1.12\times 10^{-10}\right)\]
\[x=0.64 \times 10^{-10}m\]
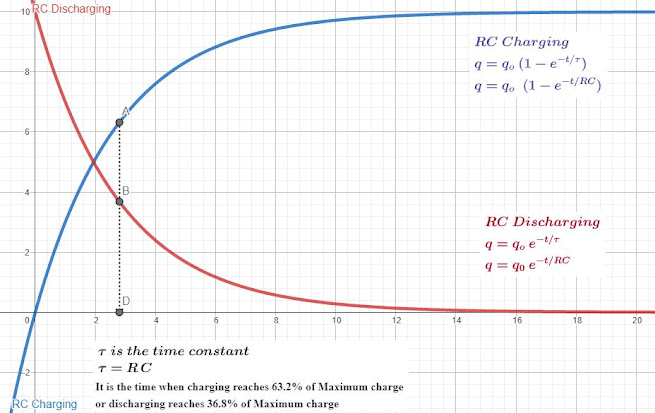
12P07B RL RC Charging Discharging Transient Currents
Change the resistance value R and the Capacitance value C in the slider
to study how the curve changes,
to observe how quickly charging and discharging are happening,
to understand what is the time constant.
Change the resistance value R and the Inductor value L in the slider
to study how the curve changes,
to observe how quickly charging and discharging are happening,
to understand what is the time constant.
Preeti reached the metro station and found that the escalator was not working. She walked up the stationary escalator in time t1. On other days, if she remains stationary on the moving escalator. then the escalator takes her up in time t2. The time taken by her to walk up on the moving escalator will be:
Problem 7. Preeti reached the metro station and found that the escalator was not working. She walked up the stationary escalator in time t1. On other days, if she remains stationary on the moving escalator. then the escalator takes her up in time t2. The time taken by her to walk up on the moving escalator will be: [NEET 2017]
(a) t1t2
t2−t1
(b) t1t2
t2+t1
(c) t1 − t2
(d) t1+t2
2
A particle covers half of its total distance with speed $v_1$ and the rest half distance with speed $v_2$. Its average speed during the complete journey is
Problem 6. A particle covers half of its total distance with speed $v_1$ and the rest half distance with speed $v_2$. Its average speed during the complete journey is [NEET 2011M]
(a) $\frac {v_1 v_2}{v_1 + v_2}$
(b) $\frac {2 v_1 v_2}{v_1 + v_2}$
(c) $\frac {2 v_1^2 v_2^2}{v_1^2 + v_2^2}$
(d) $\frac {v_1 + v_2}{2}$
\[Avg. Speed = \frac {Total \; distance}{Total \; time}\]
\[ = \frac {\frac{d}{2} + \frac {d}{2}}{\frac{d/2}{v_1}+\frac{d/2}{v_2}}\]
\[=\frac{2 v_1 v_2}{v_1+v_2}\]
A car moves from X to Y with a uniform speed $v_u$ and returns to Y with a uniform speed $v_d$. The average speed for this round trip is
Problem 5. A car moves from X to Y with a uniform speed $v_u$ and returns to Y with a uniform speed $v_d$. The average speed for this round trip is [NEET 2007]
(a) $\sqrt{v_u v_d}$
(b) $\frac{v_d v_u}{v_d + v_u}$
(c) $\frac{v_d + v_u}{2}$
(d) $\frac{2 v_d v_u}{v_d + v_u}$
If a car at rest accelerates uniformly to a speed of 144 km/h in 20 s, it covers a distance of
Problem 4. If a car at rest accelerates uniformly to a speed of 144 km/h in 20 s, it covers a distance of [NEET 1997]
(a) 2880 m
(b) 1440 m
(c) 400 m
(d) 20 m
A bus travelling the first one third distance at a speed of 10 km/h, the next one third at 20 km/ h and the last one-third at 60 km/h. The average speed of the bus is
Problem 3. A bus travelling the first one third distance at a speed of 10 km/h, the next one third at 20 km/ h and the last one-third at 60 km/h. The average speed of the bus is [NEET 1991] 
(a) 9 km/h
(b) 16 km/h
(c) 18 km/h
(d) 48 km/h
A car moves a distance of 200 m. It covers the first half of the distance at speed 40 km/h and the second half of distance at speed v. The average speed is 48 km/h. Find the value of v
Problem 2. A car moves a distance of 200 m. It covers the first half of the distance at speed 40 km/h and the second half of distance at speed v. The average speed is 48 km/h. Find the value of v [NEET 1991]
(a) 56 km/h
(b) 60 km/h
(c) 50 km/h
(d) 48 km/h
A car covers the first half of the distance between two places at 40 km/h and other half at 60 km/h. The average speed of the car is [NEET 1990]
Problem 1. A car covers the first half of the distance between two places at 40 km/h and other half at 60 km/h. The average speed of the car is [NEET 1990]
(a) 40 km/h
(b) 48 km/h
(c) 50 km/h
(d) 60 km/h
The angle between A and B is theta. The value of the triple product A.(B X A) is
The angle between A and B is theta. The value of the triple product A.(B X A) is
The magnitudes of vectors A, B and C are 3,4 and 5 units respectively. If A + B = C , then the angle between A and B is
NEET 1988
The magnitudes of vectors $\vec{A}, \vec{B} \; and \; \vec{C} $ are 3,4 and 5 units respectively. If $\vec{A} + \vec{B} = \vec{C}$ , then the angle between $\vec{A} \; and \; \vec{B}$ is
Pythagoras triplet $3^2 + 4^2 = 5^2$
So the angle will be $90^o$ between $\vec{A} \; and \; \vec{B}$
Subscribe to:
Posts (Atom)