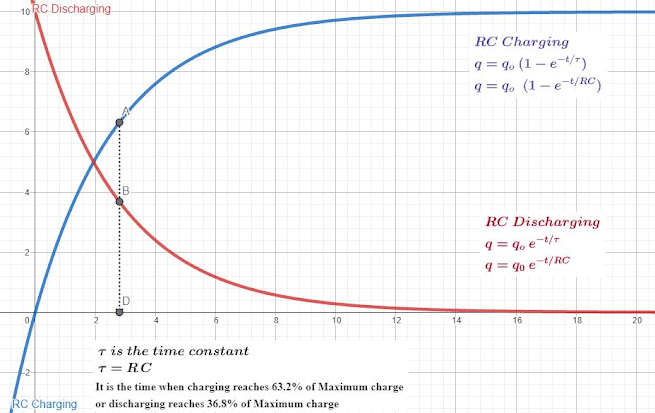
12P07B RL RC Charging Discharging Transient Currents
Change the resistance value R and the Capacitance value C in the slider
to study how the curve changes,
to observe how quickly charging and discharging are happening,
to understand what is the time constant.
Change the resistance value R and the Inductor value L in the slider
to study how the curve changes,
to observe how quickly charging and discharging are happening,
to understand what is the time constant.
Preeti reached the metro station and found that the escalator was not working. She walked up the stationary escalator in time t1. On other days, if she remains stationary on the moving escalator. then the escalator takes her up in time t2. The time taken by her to walk up on the moving escalator will be:
Problem 7. Preeti reached the metro station and found that the escalator was not working. She walked up the stationary escalator in time t1. On other days, if she remains stationary on the moving escalator. then the escalator takes her up in time t2. The time taken by her to walk up on the moving escalator will be: [NEET 2017]
(a) t1t2
t2−t1
(b) t1t2
t2+t1
(c) t1 − t2
(d) t1+t2
2
A particle covers half of its total distance with speed $v_1$ and the rest half distance with speed $v_2$. Its average speed during the complete journey is
Problem 6. A particle covers half of its total distance with speed $v_1$ and the rest half distance with speed $v_2$. Its average speed during the complete journey is [NEET 2011M]
(a) $\frac {v_1 v_2}{v_1 + v_2}$
(b) $\frac {2 v_1 v_2}{v_1 + v_2}$
(c) $\frac {2 v_1^2 v_2^2}{v_1^2 + v_2^2}$
(d) $\frac {v_1 + v_2}{2}$
\[Avg. Speed = \frac {Total \; distance}{Total \; time}\]
\[ = \frac {\frac{d}{2} + \frac {d}{2}}{\frac{d/2}{v_1}+\frac{d/2}{v_2}}\]
\[=\frac{2 v_1 v_2}{v_1+v_2}\]
A car moves from X to Y with a uniform speed $v_u$ and returns to Y with a uniform speed $v_d$. The average speed for this round trip is
Problem 5. A car moves from X to Y with a uniform speed $v_u$ and returns to Y with a uniform speed $v_d$. The average speed for this round trip is [NEET 2007]
(a) $\sqrt{v_u v_d}$
(b) $\frac{v_d v_u}{v_d + v_u}$
(c) $\frac{v_d + v_u}{2}$
(d) $\frac{2 v_d v_u}{v_d + v_u}$
If a car at rest accelerates uniformly to a speed of 144 km/h in 20 s, it covers a distance of
Problem 4. If a car at rest accelerates uniformly to a speed of 144 km/h in 20 s, it covers a distance of [NEET 1997]
(a) 2880 m
(b) 1440 m
(c) 400 m
(d) 20 m
A bus travelling the first one third distance at a speed of 10 km/h, the next one third at 20 km/ h and the last one-third at 60 km/h. The average speed of the bus is
Problem 3. A bus travelling the first one third distance at a speed of 10 km/h, the next one third at 20 km/ h and the last one-third at 60 km/h. The average speed of the bus is [NEET 1991] 
(a) 9 km/h
(b) 16 km/h
(c) 18 km/h
(d) 48 km/h
A car moves a distance of 200 m. It covers the first half of the distance at speed 40 km/h and the second half of distance at speed v. The average speed is 48 km/h. Find the value of v
Problem 2. A car moves a distance of 200 m. It covers the first half of the distance at speed 40 km/h and the second half of distance at speed v. The average speed is 48 km/h. Find the value of v [NEET 1991]
(a) 56 km/h
(b) 60 km/h
(c) 50 km/h
(d) 48 km/h
A car covers the first half of the distance between two places at 40 km/h and other half at 60 km/h. The average speed of the car is [NEET 1990]
Problem 1. A car covers the first half of the distance between two places at 40 km/h and other half at 60 km/h. The average speed of the car is [NEET 1990]
(a) 40 km/h
(b) 48 km/h
(c) 50 km/h
(d) 60 km/h
The angle between A and B is theta. The value of the triple product A.(B X A) is
The angle between A and B is theta. The value of the triple product A.(B X A) is
The magnitudes of vectors A, B and C are 3,4 and 5 units respectively. If A + B = C , then the angle between A and B is
NEET 1988
The magnitudes of vectors $\vec{A}, \vec{B} \; and \; \vec{C} $ are 3,4 and 5 units respectively. If $\vec{A} + \vec{B} = \vec{C}$ , then the angle between $\vec{A} \; and \; \vec{B}$ is
Pythagoras triplet $3^2 + 4^2 = 5^2$
So the angle will be $90^o$ between $\vec{A} \; and \; \vec{B}$
Coulomb’s law for electrostatic force between two point charges and Newton’s law for gravitational force between two stationary point masses, both have inverse-square dependence on the distance between the charges and masses respectively. (a) Compare the strength of these forces by determining the ratio of their magnitudes (i) for an electron and a proton and (ii) for two protons. (b) Estimate the accelerations of electron and proton due to the electrical force of their mutual attraction when they are 1 Å (= $10^{-10}$ m) apart? ($m_p$ = 1.67 × $10^{–27}$ kg, $m_e$ = 9.11 × $10^{–31}$ kg)
NCERT Example 1.3
Coulomb’s law for electrostatic force between two point charges and
Newton’s law for gravitational force between two stationary point
masses, both have inverse-square dependence on the distance between
the charges and masses respectively. (a) Compare the strength of
these forces by determining the ratio of their magnitudes (i) for
an electron and a proton and (ii) for two protons. (b) Estimate
the accelerations of electron and proton due to the electrical force
of their mutual attraction when they are 1 Å (= $10^{-10}$ m) apart?
($m_p$ = 1.67 × $10^{–27}$ kg, $m_e$ = 9.11 × $10^{–31}$ kg)
If $10^9$ electrons move out of a body to another body every second, how much time is required to get a total charge of 1 C on the other body?
NCERT Example 1.1 If $10^9$ electrons move out of a body to another body every second, how much time is required to get a total charge of 1 C on the other body?
How much positive and negative charge is there in a cup of water?
NCERT Example 1.2 How much positive and negative charge is there in a cup of water?
Home
Physics is a multi dimensional subject and has to be studied from many different aspects. The purpose of this website is to provide students of class 11, 12 and entrance exam preparers with high quality study materials and useful resources.
Guidelines and FAQs for Students:
For CBSE and State Board exam success: Steps 1, 2, 3 are compulsory. Step 4 good to do.
Step 1: Theory, Concepts, Derivations:
CBSE or State board text books, Handbooks, Chapterwise Study (Useful simulations and collection of videos provided here), Study Notes.
CBSE or State board text books, Handbooks, Chapterwise Study (Useful simulations and collection of videos provided here), Study Notes.
Step 2: Numerical Practice: Examples, Exercises.
Solve the Numerical from your text book.
Solve the Numerical from your text book.
Step 3: Numerical Practice: Chapter wise past paper questions
Any one of the publishers such as Arihant, MTG, XAM Idea.
Any one of the publishers such as Arihant, MTG, XAM Idea.
For Entrance exam success: Steps 4, 5 are compulsory for NEET, JEE Main, VITEEE, Amrita AEEE, KVPY, CUET etc. Step 6 compulsory for IIT aspirants.
Step 4: Numerical Practice:
Competency Based Questions, Exemplar Questions from NCERT website
Step 5: Numerical Practice:
Chapterwise NEET Past paper Questions, Chapterwise JEE Main Past paper Questions.
Chapterwise PDF downloads provided here. Arihant or MTG publications are good.
Step 6: Numerical Practice:
JEE Advanced Past paper Questions,
Practice questions from Concepts of Physics, HC Verma.
Above steps can be equally applied for other subjects such as Mathematics, Chemistry and Biology.
How much Physics should I do?
One hour of physics per day,
Above steps can be equally applied for other subjects such as Mathematics, Chemistry and Biology.
How much Physics should I do?
One hour of physics per day,
10 numerical problems per day,
2 to 3 weeks per chapter,
Approx. 100 problems per chapter,
Approx. 14 chapters in one year of class 11,
Approx. 14 chapters in one year of class 12.
Do I need a teacher to learn Physics?
Starting from Galileo and then Newton, Faraday, Edison, Tesla, Einstein, CV Raman, we have some 400 years of Physics discoveries packed into two years of 11th, 12th and entrance exam preparation. You can study from your school teacher alone. It is possible. But most students will need a tutor to help you with your difficulties initially.
How to study Physics?
You can study Physics from everywhere. Sometimes from a teacher, sometimes from textbooks, handbooks, sometimes from videos and interactive simulations, sometimes from doing some simple experiments in your home or your school, sometimes from your friend, sometimes from solving numerical problems, sometimes from nature, sometimes while going in a car or train. Physics is all around you. You just have to keep your eyes open.
Physics and Mathematics?
Physics and Mathematics are like twin sisters. They always come together. While the first part of any numerical solving is formulating the problem using Physics concepts, the second part is always mathematical simplification using Drawings, Graphs, Algebra, Trigonometry, Differentiation, Integration, Vectors etc.
Newton was not able to solve some Physics problems and he had to invent a new stream of Mathematics called Integral Calculus.
Mathematics is the language of mother nature. Physics is all about studying the nature. That's why it was called as Natural Philosophy.
Why do I have to study Physics?
Physics is the foundation for all Engineering and Science majors in college such as Mechanical, Aeronautical, Electrical, Electronics, Structural, Nuclear Engineering, Architecture, Integrated M.Sc. Physics, Energy Physics, Applied Physics, Photonics, Reactor Physics, Biophysics etc.
Students with proper physics foundation, do very well in Engineering majors. Engineering is all about problem solving. So get used to physics problem solving if you are planning to get into Engineering.
I find Physics problems very difficult?
Everything is difficult, before it becomes easy. Just like any other skills such as swimming, driving, speaking new language, Physics is also difficult to begin with.
"Remember, no problem is difficult. Once you understand the theory, each problem will become easy." - Dr. H.C. Verma
I am afraid. I make lot of mistakes?
Newton has made lot of mistakes. Einstein has made lot of mistakes. The good news is we are all allowed to make mistakes and then correct them. It's the first step to arrive at a solution.
For the Love of Physics
11P03 Motion in a Plane 2D
Circular Motion
Maximum Safe speed while taking a turn in Level Road and Banked Road.
Subscribe to:
Posts (Atom)